テスト収束の予測

開発

はじめに

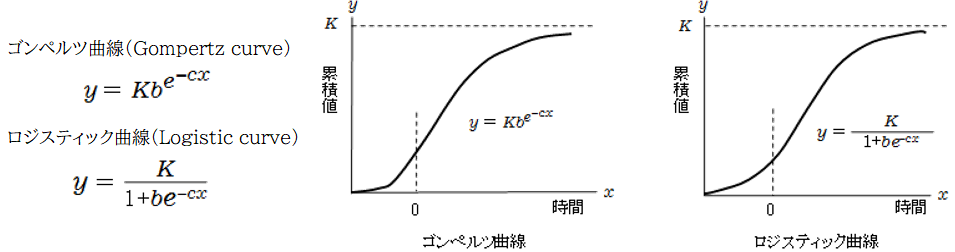
予測系の指標として成長曲線が用いられ、代表的なものに、ゴンペルツ曲線（Gompertz curve）
とロジスティック曲線（Logistic curve）があります。

.png

インターネットが外部と繋がっている環境では、ツールや計算サイトを利用可能ですが、
お客様の環境によっては、外部への接続を遮断された環境や、セキュリティのルール上
ツールのダウンロードが制限されている環境で開発することがあります。

そのような環境では自力で計算する必要があるので、ここに掲載し、その考え方を解説します。

考え方

　実測データが有るとき、をで変換しを常用対数に変換する。
　　　　　
　A,Bを下記数式で計算しておくと、
　　　　 .png
　
　で算出できる。また、実測データがN個ある場合、N番目のデータをとすると
　　　　
　でゴンペルツ曲線を使って予測が可能です。

ロジスティック曲線は解法が難解になるので、ここでは、ゴンペルツ曲線で予測する
ことにします。
ゴンペルツ曲線の両辺の常用対数を取ります。
　　　

A,Bが決まれば予測線を引くことができます。実測データが有るとき、
ととの差が０になるAとBが見付かれば、ゴンペルツ曲線と一致します。

データ数がｎ個あるとき、誤差は、の総和になりますが、
このままだと、プラス誤差とマイナス誤差で相殺されてしまうので、
２乗して誤差の大きさが０になることを考えます。

即ち、誤差が最小誤差になるAとBを求ます（最小２乗誤差）。
誤差Eが最小になるのは、微分して０になるときで、求めたいのはAとBなので、
誤差EをAとBでそれぞれ偏微分して０になることをます。
　　

AとBの連立方程式となるので、これを解くと
　　　
A=logK、B=logbと置いたので、で、Kとbが計算できる。
cについては、X＝-1の時を考えると

は、実測値がｎ個あるとき、ｎ番目の値を使います。

以上から、K,b,cを使って、実測値ｎ番以降を、X＝０以降から予測値が算出可能となります。
ゴンペルツ曲線はKに向かって収束していくので、実績からどの位で収束するのか、
また、収束するのにどのくらい時間が掛かるのかを予測することができます。